NMR signals are usually electrical signals in the radio-frequency (rf) region. In this project, we up-convert the rf signals to an optical regime, aiming at improving the detection sensitivity of NMR as compared to the traditional detection scheme.
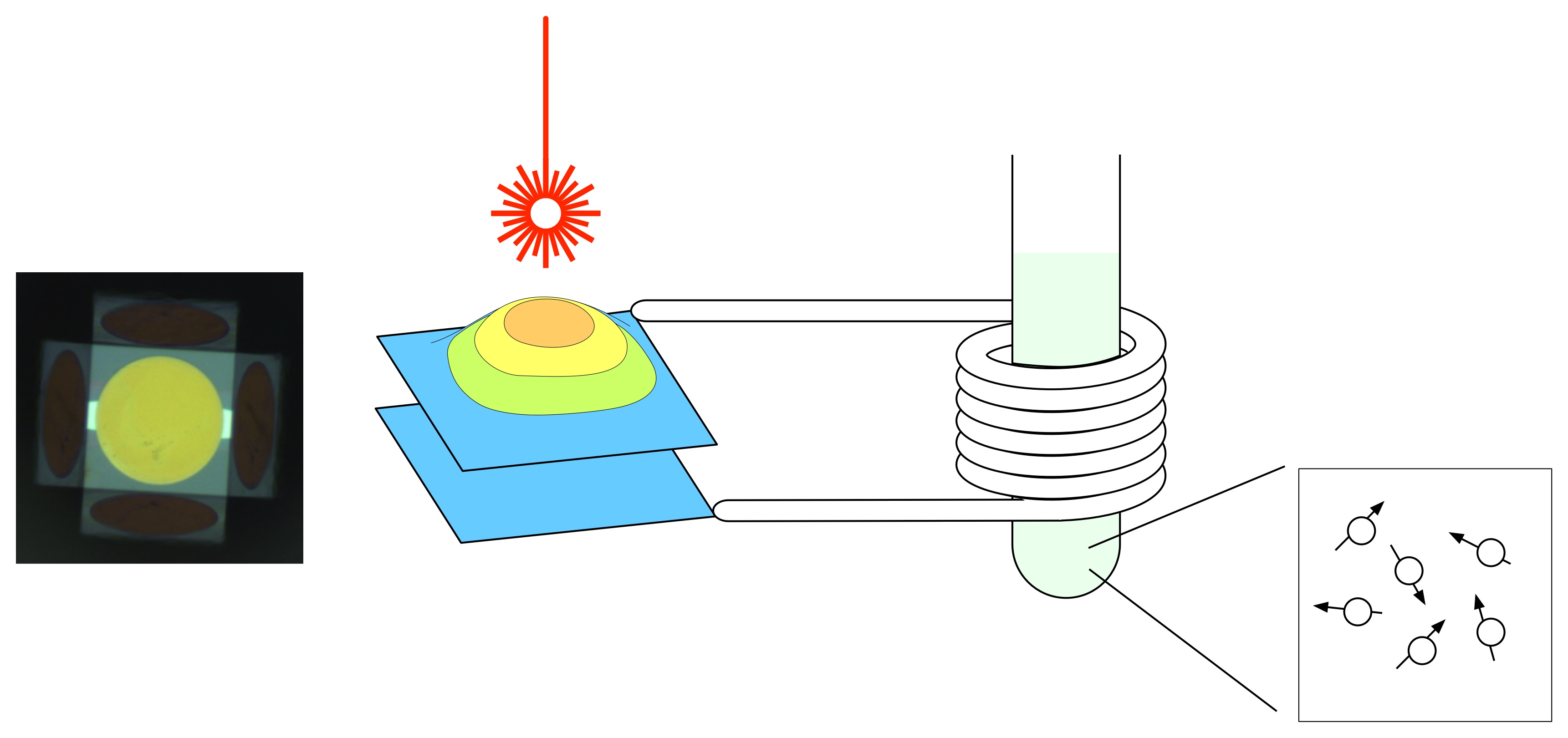
We develp rf-to-light signal transducers using a metal-coated, high-stress silicon nitride membrane oscillator. The metal layer, which is vacuum deposited on the membrane oscillator, plays two roles, namely, an electrode of a capacitor, and an optical mirror. The capacitor and an inductor form an rf resonant circuit, whreas the mirror serves for one of the two mirrors that form an optical cavity. Electromotive force due to nuclear induction causes Coulomb attraction between the electrodes of the capacitor, thereby affecting the mechanics of the oscillator. In turn, the displacement of the membrane due to oscillation changes the length of the optical cavity. It follows that the light incident into and reflecting back from the optical cavity is modulated according to the profile of the nuclear induction signal. We named this new strategy of NMR signal detection as Electro-Mechano-Optical NMR, or EMO NMR, as the signal surfs on the electrical, the mechanical, and finally the optical carriers. We succeeded in proof-of-principle demonstration of EMO NMR in 2016. Since then we have been working on EMO NMR actively, to improve its performance and toward applications to NMR analyses.

Finding NQR signals has been a challenge, because the frequency of NQR can scatter over a wide spectral range, often exceeding the bandwidth that excitation rf pulses can provide. Accordingly, one needs to repeat pulse sequence with stepwide increments of the carrier frequency.
In this project, we developed an efficient method to look for NQR signals. The key idea is to combine the rapid scan technique with frequency comb. As well known in optics, the bandwidth of carrier wave can be extendend by frequency comb. Here we demonstrated extension of the excitation bandwidth of rapid-scan pulse over several times by applying comb modulation. What is more, the comb modulation creates gaps in the excitaion pulse that can be utilized for windows of signal acquisition.
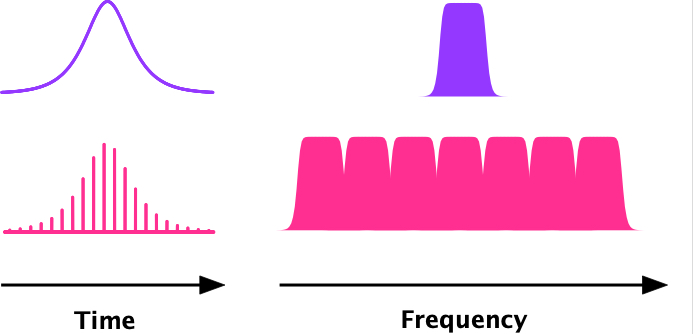
Now that comb-modulated rapid scan realizes simultaneous wide-band excitation and signal acquisition, the bandwidth of data sampling remains limited. Thus, it is not possible to tell whether the signal, if found, is a real one or an aliased one. You cannot determine the NQR frequency yet. Nevertheless, the exsintence or absence of the signal within the excitation bandwidth can be strong information. If and only if the sign of the signal has been found, we proceed to another step of what we call fine survey. In the case that the signal is not found, you can simply skip the fine survey and proceed to the next unexploed frequency regions. The fine survey uses the same excitation scheme, namely, comb-modulated rapid scan. But this time we are equipped with information that the signal, or the transverse magnetization, develops at some point during the excitation period. Right at this moment, the omplementation of the comb-modulated rapid scan is aborted, and signal acquisition is started with a sampling interval short enough for coverinng the entire excitation bandwidth. Now we can acquire the NQR signal and unambiguously determine the resonance frequency!
We showed that such a two-step scheme of serching for NQR signals is quite efficient.
We published a paper on this subject in PCCP (Physical Chemistry Chemical Physics), which was chosen as one of 2020 HOT Articles!
Y. Hibe, Y. Noda, K. Takegoshi, K. Takeda,
Rapid survey of nuclear quadrupole resonance by broadband excitation with comb modulation and dual-mode acquisition, Phys. Chem. Chem. Phys. 22 (2020) 25584–25592,
10.1039/D0CP05309K

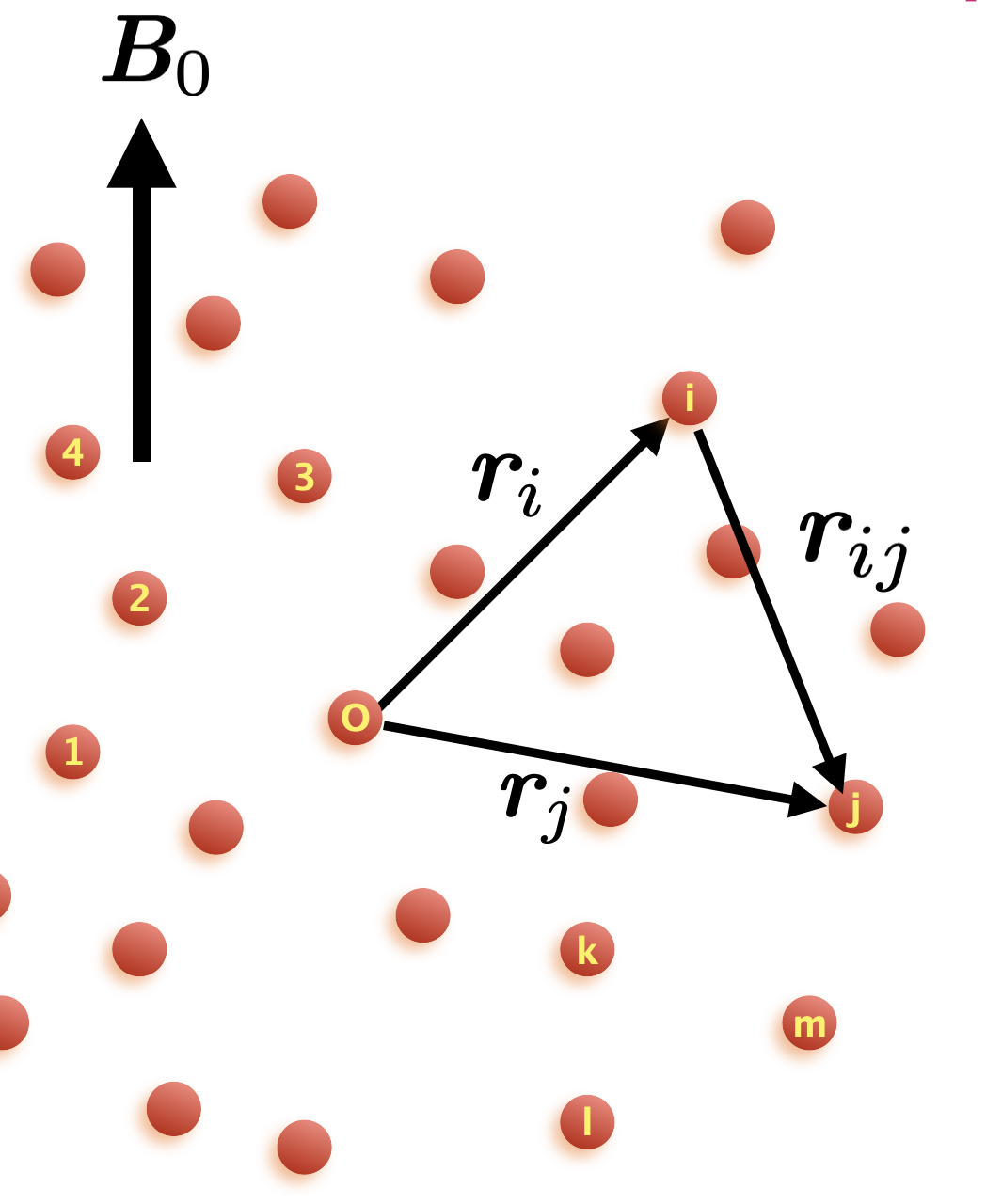
Diffusion is a process of transportation in space according to a diffusion equation. Examples of diffusion include "literal" diffusion of particles and thermal conduction. In the context of nuclear magnetism and solid-state NMR, nuclear spin diffusion, or simply spin diffusion, indicates spatial transportation of nuclear-spin magnetizaion, or equivalently, nuclear-spin polarization, that obeys diffusion equation. Several decades has now passed since the idea of nuclear-spin diffusion was put forth in 1940's, but the concept is hardly obsolete today. On the contrary, the significance of spin diffusion in solid-state NMR has been and will continue to be profound, in terms of spin relaxation and dynamic nuclear polarization in solids.
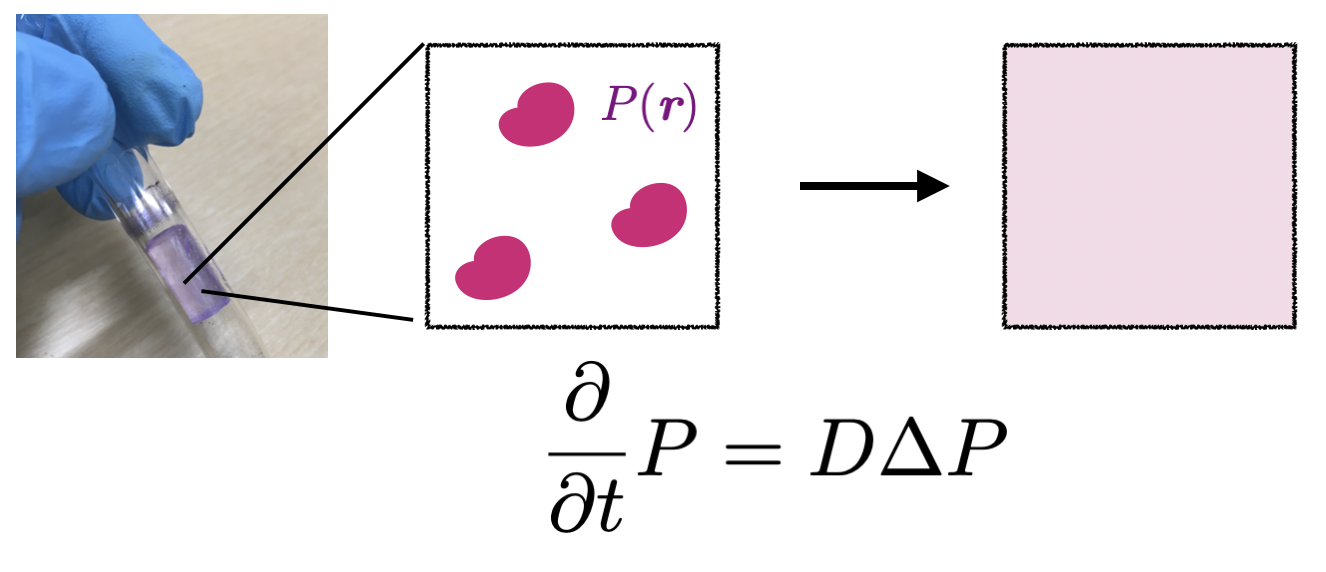
The driving force of spin diffusion is the network of dipolar inteactions among like spins. In turn, the dipolar inteaction is completely characterised by the spatial coordinates of the nuclear spins. It follows that the spin-diffusion coefficient that measures the rate at which the nuclear magnetization is transported is determined solely by the geometry of the system. This has long been a common belief over decades.
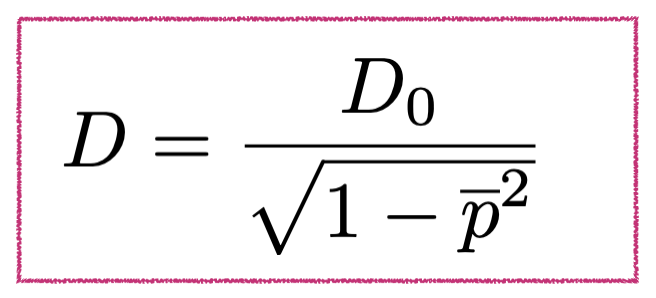
In our recent studies on spin diffusion, we came to believe that this is not always the case, in particular when the spin system is hyperpolarized. So far, theories on spin diffusion relied on high temperature approximation. This means that the theory is valid when the spin polarization is much lower than unity, while what would happen when the spins are hyperpolarized has been unclear. We studied the Lowe-Gade formula, an established formula for deriving the spin-diffusion coefficient from the coordinates of the relevant spins, and extended the theory to hyperpolarized cases. We came to a conclusion that the spin-diffusion coefficient would increase as the spin polarization is increased to very high values close to unity. That is, spin-diffusion would accelerate when the spins are hyperpolarized. Nowadays, dynamic nuclear polarization has become widespread. In this sense, our study can provide an important insight in the transportation of spin magnetization.
A paper on speedup of spin diffusion in hyperpolarized solids has been published New Journal of Physics.
Y. Wang, K. Takeda,
Speedup of nuclear spin diffusion in hyperpolarized solids,
New J. Phys. 23 (2021) 073015,
10.1088/1367-2630/ac0d6e