超臨界流体中における化学反応と分子ダイナミクス
気相と液相を連続的につなぐ超臨界流体をもちいた科学は、1980年代後半より飛躍的な進歩を遂げ、分離・抽出はもとより、有機合成、表面洗浄あるいは微結晶生成など多岐にわたる分野での展開を見せている。この超臨界流体を最も特徴づける性質は、臨界点近傍での大きな密度揺らぎであり、超臨界流体中に溶けている溶質分子のさまざまなプロセスに対してこの密度揺らぎがどのように反映されるのかが、これまでの超臨界流体の物理化学の中心課題であった。一般に、臨界密度付近の中密度領域では、溶質分子の周りに溶媒分子がバルクの密度以上に集まってくるという局所密度増加がみられる。このようないわゆる密度揺らぎの効果は、部分分子容のように直接的にあらわれてくる場合もあるが、多くの観測量においては必ずしも単純な形で反映されるわけではない。観測量がどのような分子間距離での相互作用を反映するかによって、密度揺らぎの効果あるいは局所密度増加のみえかたは顕著に変わってくるのである。
我々はこのような超臨界流体、特にその臨界密度付近の中密度領域での溶媒効果の問題に関連して、特に以下の項目を中心に研究を進めている。
５．超臨界水での共鳴ラマン分光
実験手法としては、ひろい時間領域にわたる時間分解分光法(フェムト秒から秒まで)を中心に、共鳴ラマン分光などを超臨界流体に適用している。時間分解分光法としては、過渡吸収、蛍光、過渡回折格子法などを中心に研究を進めている。
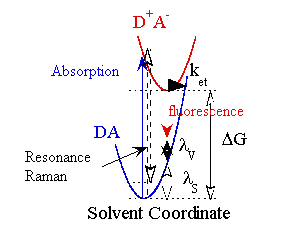
超臨界流体での溶媒和に関連して、数多くの分子の電子遷移スペクトルの研究が報告されているが、その多くはピークの密度依存性の定性的な議論、あるいは吸着モデルを用いた単純な局所密度による議論にとどまり、分子内振動構造や、溶媒和再配向エネルギー、あるいは電子移動速度の密度変化を検討したものはほとんど存在しなかった。我々は、共鳴ラマン分光法、ピコ・フェムト秒の過渡吸収測定を超臨界流体に適用し、これらの問題に対し典型的な答えをだしてきた。
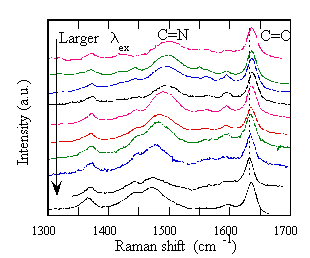
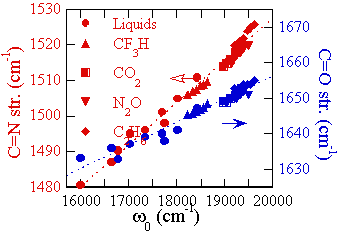例えば典型的なソルバトクロミズムを示す分子であるフェノールブルーに対して、超臨界流体を含む種々の溶媒中での電子遷移吸収および共鳴ラマンの測定をおこない、電子遷移エネルギーと分子内振動数の溶媒によるシフト及び揺らぎに線形の相関がある実験的証拠をはじめて提示した(図は種々の流体中でのラマンストークスシフトと吸収のピークを比較したもの)。さらに、ラマンストークスシフトが、励起波長に依存して変化するという新奇な現象を発見した(ラマンスペクトル図はメタノール中でのラマンストークスシフトの励起波長依存性。励起波長は457.9nmから647nm)。超臨界流体を用いた研究から、この現象は電子遷移エネルギーの揺らぎと振動数の揺らぎが相関していることに起因することを明らかにし、理論的に実験結果を説明することに成功している。さらに、これらの情報をもとに電子励起状態の寿命の議論もおこなっている。
また、ヘキサメチルベンゼンとテトラシアノエチレンからなる電荷移動錯体における電子励起状態からの逆電子移動反応速度を、ピコ秒の過渡吸収法により種々の超臨界流体中ではじめて決定した。この錯体は四塩化炭素中の共鳴ラマンの検討から、無極性溶媒での特異な挙動（無極性溶媒でも溶媒再配向エネルギー大きい（Ca.2650cm-1））が指摘されている分子であるが、気相から液相に近い密度領域までスペクトルの密度変化ならびに反応速度を検討することにより、両対中における溶媒和再配向エネルギーの詳細な評価ができる。測定の結果、反応速度はMarcus/Jortnerの理論に基づく吸収スペクトルの解析から見積もった反応の自由エネルギーと溶媒の再配向エネルギーとによく相関していることがあきらかとなり、無極性の超臨界流体では特に再配向エネルギーが大きいわけでもなく、また臨界点近傍の密度揺らぎが電子移動反応速度にあまり顕著な影響を与えていないことがわかった。
一方で、これらの実験で見積もられた溶媒再配向エネルギーの密度変化を分子論的に解釈するために、相互作用サイトモデルに基づく積分方程式理論を溶媒再配向エネルギーの密度変化の計算に適用をおこなってきた。具体的には双極子(1.4D)を持ったダンベル分子からなる溶媒中に、同じ大きさのダンベル分子を溶質として溶かし込み、その双極子モーメントを1.4Dから4.2Dまで変化させたときに、溶媒和の自由エネルギー差(ΔA)と垂直遷移のエネルギー(ΔUt)がどのように変化するか計算した。その結果、実験的に見られるスペクトルシフトを定性的に再現していることができた。そこで、個々の溶媒密度での溶媒和の状況を検討するために、溶質分子に作用する反作用場の大きさを溶質の双極子の大きさをかえて計算し、溶媒１個あたりの量にして比較した結果を図に示す。0.5以上の密度領域では、溶質の電荷に対して反作用場はおおむね線形に増大していくが、それよりも低い密度領域では非常に非線形性が強いことがわかる。また溶媒１個あたりの反作用場の大きさも密度によって異なる。このことは、溶媒近傍の分子一個あたりに与える溶媒和のエネルギーが高密度領域と低密度領域で大きくことなることを示している。これは高密度領域におけるパッキングの効果で溶媒分子が溶質分子に対して最安定の位置を取れないことに起因する。このことは、スペクトルの密度変化を説明するのに従来から推奨されてきた単純な局所密度の概念は適用できないこと示している。また、このような現象を確かめるために、クマリン色素の蛍光ストークスシフトの詳細な検討をおこない、理論もモデルの妥当性の検討を行っている。
これらの詳細は論文を参考されたい。
2.振動緩和過程
溶液中で励起分子の振動緩和がどのようなメカニズムで起こっているかを理解することは、溶液物理化学の中心課題のひとつであり、これまで多くの実験がおこなわれ、種々の理論が提唱されてきた。そのうち古くから提唱されているIBCモデル(Isolated Binary Collision Model)は、気相領域における振動緩和の理屈を凝縮相に適用したものであり、振動緩和の速度は、衝突頻度Zと衝突あたりに失うエネルギーの割合ΔEに比例するとするものである。このIBCモデルの妥当性に関して種々の実験的、理論的研究が行われてきたが、凝縮相で衝突頻度の評価の困難さのため、未だ最終的な決着はついていない状況である。我々は同一分子の電子基底状態と励起状態での振動エネルギー緩和速度を比較することによりIBCモデルの妥当性の検証をおこなってきた。
アズレンはS2状態から比較的長寿命(ca.
1.6 ns)の蛍光をだす分子であり、その蛍光の線形が過剰エネルギーに依存して変化することが知られている。したがって、蛍光スペクトルの線形を光励起後から時間分解で測定し、その線形から過剰エネルギーを評価して振動エネルギー緩和速度を調べることが可能となる。図はエタン中で,283nmで励起後の蛍光スペクトルの時間変化を示したものである。時間の経過にしたがって蛍光スペクトルに構造がはっきりとあらわれてくるが、この変化はちょうど過剰エネルギーの減衰と対応しており、ここからエネルギー緩和速度を求めることができる。
このようにして求めたエタン中におけるS2状態での振動エネルギー緩和速度と、文献の基底状態の振動エネルギー緩和速度とを比較すると、S2状態の振動緩和速度の密度変化と基底状態の振動緩和速度の密度依存性は非常に類似していることがわかった。ただし、おなじ溶媒密度で比較すると励起状態の緩和速度のほうが1.5倍程度速いことがわかる。二酸化炭素およびキセノン中でも同様の傾向が得られた。この結果は、振動緩和速度にたいするIBCモデルとは矛盾しない。すなわち、緩和速度の密度変化は衝突頻度の密度依存性できまり、基底状態とS2状態での緩和速度の差は衝突あたりのエネルギー失活の効率を反映していると考えられる。
溶媒との相互作用が弱い系においては、振動緩和速度は振動の基準座標方向に作用する溶媒からの揺動力F(t)の時間相関関数Γ(t)(<F(0)F(t)>)をフーリエ変換した振動数ω の実数成分に比例する。一般に分子内振動の振動数は溶媒の運動と比較して速いので、揺動力の相関関数Γ(t)のうち、その初期の部分が振動緩和に効果的な領域となる。従って、Γ(t)の初期部分の関数形が溶媒の密度に依存しなければ、IBC的な描像が成立する。
この点を検証するために我々は簡単なモデル計算を行った。具体的にはLennard-Jonesポテンシャルで相互作用する流体中に溶質分子1個入れたときの、溶質分子に作用する等方的な揺動力の相関関数を計算した。溶媒の温度はLJ単位で1.5、溶質溶媒の引力的相互作用は溶媒間の二倍にしてある。図には異なる3つの溶媒密度での結果が示してあるが、その初期過程の関数形が溶媒の密度にほとんど依存しない。これはIBC的な描像が成り立ちうることを示している。われわれはまた、斥力相互作用部分の揺らぎの評価をおこない、溶質溶媒が斥力的な相互作用をする領域において溶媒分子間に相関がないことがこのような描像を成り立たせていることを明らかにした。
これらの詳細は論文を参考されたい。
一方で、過渡回折格子法を用いて溶媒側からエネルギーダイナミクスを検討するとまた違った情報が見えてくる。（時間分解グレーティングの詳細については寺嶋先生のホームページを参照。）
内容の詳細については現在構築中
流体中で二原子分子が光解離するような反応系を考える。この分子の光解離の量子収率はその分子のポテンシャル面と周りの溶媒からくるCage効果の寄与で議論することができる。一般に、溶質分子の周りに溶媒分子がタイトに詰まっているほど、光解離の量子収率は下がることが期待される。では、溶質分子のまわりに局所的な溶媒和構造が生成する超臨界流体の中密度領域においてこのような量子収率の減少がみられるのであろうか？このような疑問は古くからもたれ、ドイツのグループが1980年代の初頭に過渡吸収法を用いてヨウ素の光解離量子収率について詳細な検討をおこなった。その結果、二酸化炭素やエタンなどの流体では低中密度領域において極端な量子収率減少が見られた（J. -C. Dutoit et al., J. Chem. Phys.
1983, 78, 1825; Luther et al., J. Phys. Chem. 1980,
84, 3072）。われわれは、この研究を追試すべく、過渡回折格子法を用いて種々の超臨界流体中でのヨウ素の光解離量子収率の評価をおこなった。
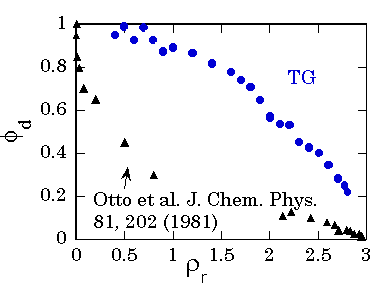過渡回折格子法では反応に伴う熱量を時間分解で検出することができるため、初期のジェミネート対の再結合による速い熱放出過程と、拡散による遅い再結合過程から生じる熱量の比を求めることで光解離の量子収率を求めることが可能となる。こうした実験の結果、過渡回折格子法では過渡吸収法でみられた異常な量子収率の密度変化を再現することはできなかった。その原因は未だ不明である。
ヨウ素のほかにも超臨界流体中でのスルフィド化合物に関する研究も行っている。
これらの詳細は論文を参考されたい。
とりあえず大森君のホームページ参照。
５.超臨界水での共鳴ラマン分光
構築中