Peierls transition refers to the phenomena in which metals undergo phase changes associated with Fermi surface instability and periodic lattice distortion due to the interaction of electrons and phonons at k = 2k_F. The Peierls transition is often called charge-density-wave transition (CDW transition), as it is associated with the formation of charge density waves in the low-temperature phase. R. E. Peierls proposed the mechanism in his famous Quantum Theory of Solids (1955) in order to elucidate why low-symmetry structures are stabilized in crystalline Sb and Bi. Later, phase transitions found in 1970s in materials with low-dimensional Fermi surfaces have shown to be driven by this mechanism.

Owing to intensive studies, it has been established that the qualitative behaviour of the Peierls transition is well characterized by the strength of electron-phonon coupling as a dominant parameter. Thus the transitions have been more often categorised simply into two classes: weak-coupling and strong-coupling types.

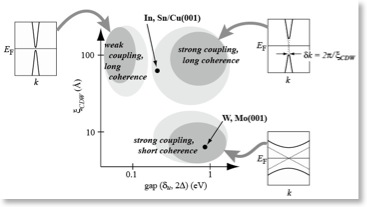
Our study have shown, however, that the classification scheme is not appropreate in understanding the transitions found on surfaces in the last decade. According to the previous model, the weak-coupling type is associated with a long correlation length and the strong-coupling type with a correlation length on the order of a lattice parameter. However, on the In/Cu(001) surface, which Nakagawa et al. showed in 2001 to undergo a Peierls-type transition at 350-400 K, is associated with an unexpectedly long correlation length while it should be categorized into the strong-coupling type.

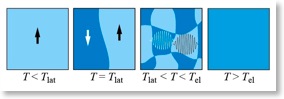Hatta et al. in our group have studied temperature dependence of the energy gap, a parameter characterizing the electron-phonon coupling, and the lattice correlation length. The result reveals the detailed behaviour of the phase transition, which differs from neither of the weak-coupling long-coherence or the strong-coupling short-coherence types, thus introducing a new member of the Peierls transition family.
（Bulletin of the Phys. Soc. Japan, 63, 178-186 (2008) [a review in Japanese]; Surf. Sci. Rep. 61, 283 (2006).)